How can I send music around in a vortex of sound without creating a model of a vortex? A major portion of the work behind the Vortex of Sound concept lies in the mathematical modelling of the shape.

Vortex Shape Inspiration

What exactly is a vortex? Merriam-Webster defines a vortex as

“a mass of fluid (such as a liquid) with a whirling or circular motion that tends to form a cavity or vacuum in the center of the circle and to draw toward this cavity or vacuum bodies subject to its action.”

Some examples of vortices include whirlpools (natural or in bottles), tornados, and hurricanes.

Past physics classes and differential equations classes hint at a few of the key assumptions I made in creating a vortex. Namely,

  1. If you take a cross-section across a vortex, perpendicular to the vacuum in the center, the particles of fluid are circling the center. In a 2-dimensional differential equations setting, you view these as arrows pointing towards a sink. Merriam-Webster’s definition above corroborates with this assumption.
  2. Conservation of mass-energy in physics, one of Newton’s Laws reminds us that we cannot create or destroy matter (ok… normally, without some combination of energy and antimatter, but that’s more advanced physics than I want to consider). At most, matter just changes forms.
    Therefore, I am assuming that once the fluid particles get into the sink at the center of the vortex, they don’t just disappear. They need to go somewhere, and in my depictions, they move vertically along the sink, and then spiral outwards from the sink as if it is a source. Some diagrams of cross-sections of hurricanes seem to support my assumption, so it is what I am going with.

Due to variables such as heat and moisture, they have some convection happening that causes extra up-down cycling that I decided not to model. Therefore, while the overall shape will look like fluid particles are cycling as they ought to physically, I will just have the fluid particles circle the sink, keeping their respective fixed radii, and none will move vertically. This also saves me from having to replace particles that have cycled out of the top of my model.

How to model the shape

Now that we know what a vortex is, let’s move on to actually modelling a vortex with an an arbitrary number of points, \( n \)!

Cross Sectional Views

Consider a 3-dimensional Cartesian coordinate system.

When looking at a cross section of the shape in the \(X-Y\) plane, the shape seen should resemble a donut. There will be a fixed inner radius but the outer radius will depend on the \(Z\) value.

Now, consider the \(Y-Z\) plane cross-section where \(x=0\).
This should look like a horizontal parabola, reflected across the \(y\)-axis. There should also be a vertical line, between \(y=0\) and the parabola, which is the eyewall of the hurricane. These two lines define the radii of various circles of motion of points. There is rotational symmetry along the \(z\)-axis.

What does this look like?

Dimensions

The initial dimensions are the following.

  • Height: \(0 - 9.5\) feet
  • Center Height: \(4.56\) feet
  • Eyewall Radius: \(10\) feet
  • Minimum Outer Shape Radius: \(20\) feet
  • Maximum Outer Shape Radius: \(100\) feet

The center height is calculated by multiplying the maximum height by a scaling factor of \(24/50\). The rest of the dimensions are calculated from diminutization of a hurricane, and substituing feet for miles.

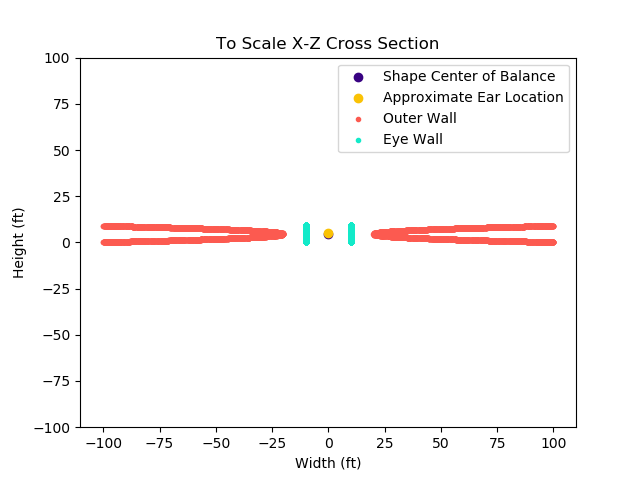
The outline of the shape, to scale, looks something like the following partial cross section of the \(X-Z\) plane. The parabola portion is very long and narrow. Graphic depicting a cross section of the storm. The horizontal, parabolic outer walls are in coral. The vertical inner walls in aqua. The indigo center of the balance of the shape is between the two aqua inner walls, and lines up horizontal with the vertices of the coral parabolas. The yellow ear indicator showing where I imagine my ear height to be roughly located lies slightly above the indigo center of balance.

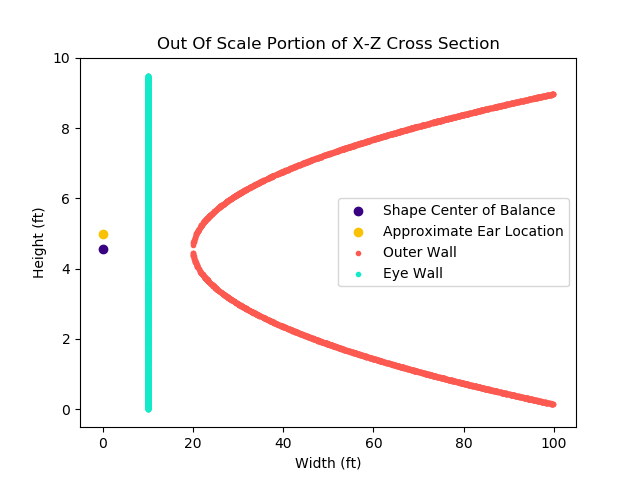
An out of scale, closer look at a portion of the cross section shows that the ears of a listener of my height should be slightly above the center of the parabola. If this cross section portion were to be rotated around the z axis, the section between the aqua inner eyewall and coral outer wall would be the body of the storm. Graphic depicting half of a cross section of the storm shape. The horizontal, coral parabola opens to the right. The vertical aqua inner walls lies to the left of the . The indigo center of the balance of the shape lies between the aqua inner wall and the z axis. The center lines up horizontally with the vertex of the coral parabolas. The yellow ear indicator showing where I imagine my ear height to be is less than a foot above the indigo center of balance.

Equations

To randomly generate points in the storm, I needed to know the equation for the inner wall, the radius of the outer wall, and the outer wall.

Eye Wall

The eye wall is always \(10\) feet from the center. There is rotational symmetry around the z-axis, because the storm rotates around its center. Therefore, any point on the eye wall can be modelled using the equation of a circle for the z’s in the correct height range.

\[x^2 + y^2 = 10^2, \forall z\in[0,9.5].\]

Radius of Outer Wall

The radius of the outer wall depends on the height, \(z\) of the point in the storm. The radius also is also always between \(20\) and \(100\) feet, due to the dimensions of the parabolic shape introduced in the section above. Therefore, we need to calculate the parabola defining the outer wall to calculate the maximum radius at a particular height.

A sideways parabola, in the \(X-Z\) plane, has the equation

\[(z-k^2) = 4p(x-h).\]

Since we want to deal with a vortex, we will have many rotations of this shape around the z axis. Therefore, we replace the \(x\) with an \(r\). To calculate the radius at a given height, we rearrange the formula, and get

\[r = \frac{(z-k)^2}{4p} +h.\]

In this case, \(z\) is the height of the point in the storm. The values \(h\) and \(k\) are determined by the vertex at \((h,k)\), which, in the \(X-Z\) plane with coordinates \((x,z)\) is \((20,4.56)\). This means that at a particular \(z\),

\[r(z) = \frac{(z-4.56)^2}{4p} +20.\]

To solve for \(r(z)\), we need to know the value of \(p\). Since the vertex of the parabola is at \((20, 4.5)\) and the distance between the \(z\) axis and the parabola, \(r\), is longest at the bottom, where the parabola hits the ground, the coordinate \((100, 0)\) also lies on the parabola. We calculate \(p\) as follows:

\[p = \frac{(z-k)^2}{4(r-h)},\\ = \frac{(z-4.5)^2}{4(r-20)},\\ = \frac{(0-4.5)^2}{4(100-20)},\\ = \frac{(-4.5)^2}{320},\\ = \frac{(-4.5)^2}{320},\\ = 0.06328125.\]

This makes the calculations of the radius at a certain height

\[r(z) = \frac{(z-4.56)^2}{4p} +20,\\ = \frac{(z-4.56)^2}{4*0.06328125} +20,\\ = \frac{(z-4.56)^2}{0.253125} +20.\]

Great! Now that we know the different radii of the outer wall and eye wall, we can generate points between the two.

Generate the shape

Generating points between the eye wall and outer wall involved following the process below for each point in the shape.

  1. Generate a height, \(z\), uniformly at random from the range \([0,9.5]\).
  2. Generate an angle, \(\theta\), uniformly at random from the range \([0,2\pi)\).
  3. Calculate the maximum possible radius, \(R(z)\) given a particular height \(z\).
  4. Generate a radius \(r\), uniformly at random between \([0,R(z)]\).
  5. The specific point lies at \((r, \theta, z)\) in cylindrical coordinates.

The resulting shape is not uniformly distributed, but the result seems sufficiently vortex shaped. If points are more likely to be closely packed together the closer they are to \(z\) value of the vertex of the parabola, I do not find this particularly problematic. I find it fitting that the most concentrated parts lie towards the center of the shape, as I imagine it is the same for an actual vortex.

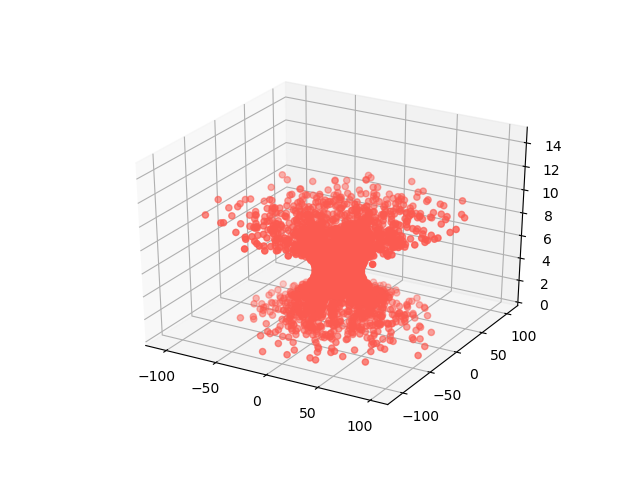
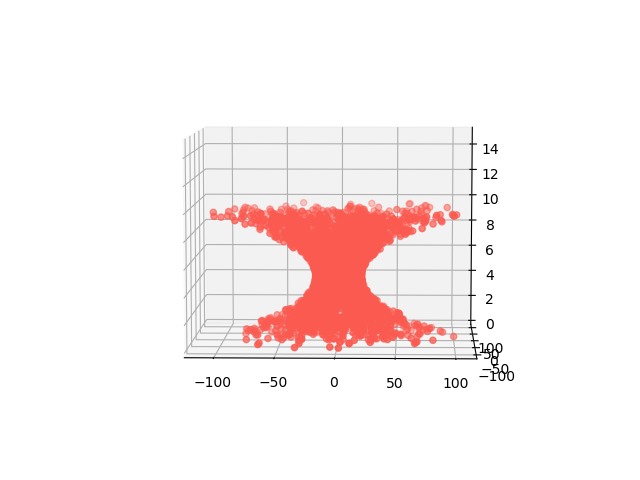
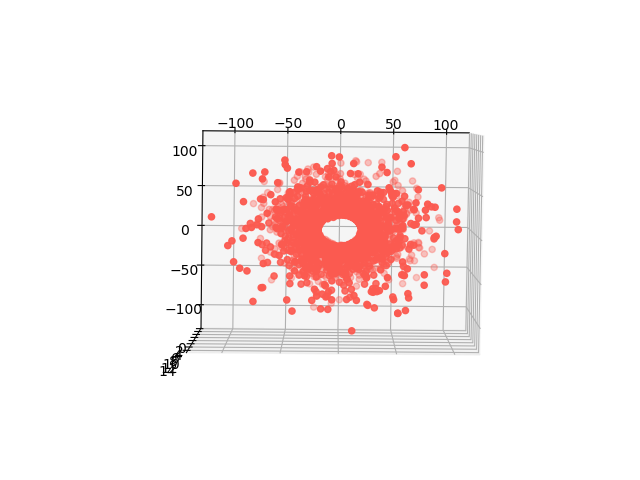
Here are an angled view, a side view, and a top-down view of the shape. Keep in mind that if the image were to scale, the images would be much wider than they are tall.

In the angled view, it is easiest to see that the vortex is densest near the vertex of the parabola defining the outer wall. Angled view of the vortex. A bunch of salmon-colored dots in the shape of a vortex. This is a 3-dimensional perspective of the shape.

The side view reassures us that the shape is vortex like. It also shows us that the vortex is slightly top heavy, due to the center of the parabola being below half of the maximum height. Side view of the vortex, which is represented by a bunch of salmon-colored dots. This is either an x-z or y-z plane view of the overal shape.

From above, we see that the eyewall exists. There will be an eye of calmness inside of the shape. Additionally, we can see that the fringes of the shape have less in them than the denser center. Top down view of the vortex, which is represented by a bunch of salmon-colored dots. This is a overhead view of the x-y plane.

Now what?

We have a basic shape. What’s next? We need to assign different instruments different dots in the shape. But that can wait until another post.

The code behind these shapes can be found on my github.